Макс. полощадь N-угольника в пространстве Опции

[Altair]

задача
Дано множество точек в простанстве.
Определить координаты n-угольника максимальной площади с вершинами в данных точках.


Если бы задача решалась на плоскости, то все тривиально - строим выпуклую оболочку и вот нам многоугольник макс. площади.
Программа:  p.pas ( 4.72 килобайт ) Кол-во скачиваний: 917

Сриншеты:


EXE и исходники в архиве:  p.zip ( 33.28 килобайт ) Кол-во скачиваний: 586


Вопрос вот в чем... какой же алгоритм стоит применить когда речь о пространстве ?
Одна из сложностей - площадь мы все равно можем считать только плоской фигуры, а сколько плоскостей надо перебрать в пространстве только для того что бы на каждой искать выпуклую облочку..
ясно что задача решается как то по другому... в какую сторону копать ?

p.s. спасибо одной девушке за любезно предоставленную задачу



То , что многоугольник обязан быть выпуклым доказывается очень просто.
Предположим что макс. площадь достигаается невыпуклым:


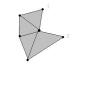
но тогда соединив точки 1 2 мы получим выпуклый, причем с большей плозадью.

[Altair]

Как вариант решения задачи, было предложенно (mo3r)
перебирать тройки точек, и для каждой тройки определить, какие вершины лежат с ними в одной плоскости, и построить их выпуклую оболочку.
Временная сложность: O(n^4*log(n)) (n^3 троек, на каджую тройку - n*log(n)).

[hardcase]

А если не перебирать все точки сразу, а построить выпуклую оболочку для всего множества, и потом к ней применить приведённый выше алгоритм?

Или можно строить не оболочку, а выбирать точки по определённому критерию - отметать все заведомо лежащие внутри фигуры точки.

Сообщение отредактировано: hardcase - 29.01.2006 16:15

[Altair]

hardcase, ты абсолютно прав, но
1. алгоритма построения выпуклой оболочки в пространстве нет.
2. если ты построишь его, то не факт , что по скорости весь алгоритм будет быстее..