я понятия не имею как оформить задачу для 9 класса не выходя за рамки темы дифференциалы функций многих переменных. спасите-помогите
 Компиляция правил для данного раздела
Компиляция правил для данного раздела
1. Заголовок темы должен быть информативным. В противном случае тема закрывается и удаляется ...
2. НЕ используйте форум для личного общения, все что не относится к обсуждению темы - на PM!
3. Одна тема - один вопрос (задача)
4. Спрашивайте и отвечайте четко и по существу!!!
| кучаТрупов |

Сообщение
#1
|
|
изувер   Группа: Пользователи Сообщений: 88 Пол: Женский Реальное имя: ann Репутация:  1 1  |
через точку В,лежащую внутри угла провести прямую так, чтобы она отсекала от угла треугольник наименьшей площади.
я понятия не имею как оформить задачу для 9 класса не выходя за рамки темы дифференциалы функций многих переменных. спасите-помогите |
  |
Ответов
| TarasBer |

Сообщение
#2
|
 Злостный любитель      Группа: Пользователи Сообщений: 1 755 Пол: Мужской Репутация:  62 62  |
Решение такое можно:
Площадь треугольника разбивается на три. Одна из них - это 4х-угольник с 2мя прямыми углами, он не зависит от проведения прямой. Сумма площадей двух других равна x*x*tg(a) + y*y*tg(b), причём даны x, y - это длины перпендикуляров из точки и сумма a+b=c - это сама величина угла. x*x*tg(a)+y*y*tg(c-a) = x*x*tg(a) + y*y*(tg©-tg(a)/(1+tg©*tg(a)) дифференцируем по tg(a) получаем x*x + y*y*(-1-tg©*tg©) / sqr(1+tg©*tg(a)) равносильно x*x/(1+sqr(tg©) = sqr(y/(1+tg©*tg(a))) x*x*sqr(cos©) = sqr(y/(1+tg©*tg(a))) x*cos© = y/(1+tg©*tg(a)) 1+tg©*tg(a) = y/(x*cos©) tg(a) = (y/(x*cosc) - 1) * ctg© = y/(x*sin©) - ctg© Угол найден, ура. Все операции построимы циркулем и линейкой. Ааа, уберите эти автозамены, мешают только. Сообщение отредактировано: TarasBer - Эскизы прикрепленных изображений 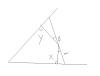
-------------------- |
Сообщений в этой теме
 кучаТрупов угол,точка,наим.площадь. 8.10.2009 18:00
кучаТрупов угол,точка,наим.площадь. 8.10.2009 18:00
 TarasBer А она вообще имеет не-матановое решение? 8.10.2009 20:17
TarasBer А она вообще имеет не-матановое решение? 8.10.2009 20:17

 sheka
А она вообще имеет не-матановое решение?
имеет… 8.10.2009 21:00
sheka
А она вообще имеет не-матановое решение?
имеет… 8.10.2009 21:00
 TarasBer Ааа, я туплю.
Если очень вкратце, то простое решин… 9.10.2009 3:16
TarasBer Ааа, я туплю.
Если очень вкратце, то простое решин… 9.10.2009 3:16
 Lapp как оформить задачу для 9 класса не выходя за рамк… 9.10.2009 5:44
Lapp как оформить задачу для 9 класса не выходя за рамк… 9.10.2009 5:44  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | 11.03.2026 5:42 |
Связь с администрацией: bu_gen в домене octagram.name








