Сумма ряда, Вот дык проблема Опции

[sheka]

Была тема на Исходниках http://forum.sources.ru/index.php?showtopic=264902

Проясните ситуацию плиз. До конца так и не понял, что значит вычислить сумму бесконечного ряда с заданной точностью...?...
Точнее не понял куда привязать точность (поиск по инету выдал кучу ссылок, но все по разному делают):
1) как то связано с самой переменной, отвечающей за сумму
2) когда по модулю текущий член оказывается меньше заданной точности.
3) когда разность между Xi и Xi - 1 оказывается по модулю меньше заданной точности...
подскажите как быть то..?...

Но ответ там как-то и не дали..

[sheka]

А какие бывают случаи? В том то и дело, что меня интересует вопрос в общем, а не "конкретная задача".
Вот, например:

[Lapp]

А какие бывают случаи? В том то и дело, что меня интересует вопрос в общем, а не "конкретная задача".
Вот, например:

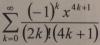
Так "в общем" тебе ответил Тарас. Ты ряды проходил или еще нет? Скорее всего нет еще.. Тогда у тебя могло сложиться неправильное представление, что ряды - это так, пустяк, просто сложение, его в первом классе проходят типо.. )) И тебе может показаться, что максимум, что с ними можно сделать - это посчитать на компе с некоторой (разумной с разных точек зрения) точностью. Если это так - это большая ошибка. Простота внешнего вида бывает обманчива..

Ряды - это самостоятельный раздел математики, в нем развитая система теорем. По ним написаны толстые книги, их исследовали очень видные математики. В курсе мат.анализа этот раздел занимает.. да до фига! (кажется, у нас был чуть не целый семестр). Ряды могут сходиться и расходиться, причем и то и другое с разной скоростью. Есть много всяких признаков сходимости/расходимости. Есть классификация рядов, и для каждого случая годятся свои оценки скорости сходимости (или их нет). Вот, например, то, что ты приаттачил - это ряд знакопеременный (название говорит само за себя). Для таких рядов есть простой признак (который доказывается), что он при условии убывания общего члена (в данном случае, x<1) сходится, и остаток ряда по модулю меньше модуля последнего члена частичной суммы (вот тебе и оценка точности). Твоя просьба объяснить "в общем случае" означает, что мы должны тебе преподать всю теорию рядов?

У меня еще такое замечание есть.. Часто задача звучит "посчитать сумму ряда с точностью", но при этом упор делается не на математику, а на программирование. И при этом подразумевается именно оценка по последнему члену (как в знакопеременных рядах). Это в общем случае совершенно неверно, но преподавателей программирования это не волнует. Я видел такое неоднократно тут, на Форуме. Такие вещи нужно выяснять непосредственно у того, кто дал задачу.