В равнобедренном треугольнике АВС угол В=100 градусам. Внутри треугольника взята точка М так, сто угол МАВ =10 градусам, а угол МВА=20 градусам. Найти угол ВМС.
Спасите!!! Вот уже 6-ой час не можем решить задачу всей семьей:
 Компиляция правил для данного раздела
Компиляция правил для данного раздела
1. Заголовок темы должен быть информативным. В противном случае тема закрывается и удаляется ...
2. НЕ используйте форум для личного общения, все что не относится к обсуждению темы - на PM!
3. Одна тема - один вопрос (задача)
4. Спрашивайте и отвечайте четко и по существу!!!
| Лена |

Сообщение
#1
|
|
Гость |
|
  |
Ответов
| Lapp |

Сообщение
#2
|
 Уникум        Группа: Пользователи Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
День добрый, Лена и Ко!
Не сердитесь, что я вынимаю на свет Божий дела давно минувших дней.. Я совершенно случайно набрел на этот тред, и меня заинтересовала задача. После получаса размышлений над ней за чашкой кофе я просто полюбил ее. Лена, не судите строго ее автора - он явно незаурядный человек, и спасибо ему за удовольствие подумать. Задача из тех, где нужно искать не общие принципы, а совпадения частных параметров. Как только это поймешь, все становится на свои места. Достаточно лишь привлечь побольше данных - в данном случае провести пару лишних линий (которые напрашиваются) и вычислить несколько углов. Потом все это сопоставить. И _очень_важно_ сделать _хороший_ чертеж! Я не пожалел усилий, хотя неточности могут быть, ибо транспортира под рукой не оказалось. Но это не важно - чертеж должен быть не идеальным а _достаточно_ хорошим. Итак, решение (кратко). Опустим высоту из В. Продолжим АМ до пересечения с ней (т. О). Угол ВМО вычисляем, как внешний в тр.АВМ, он равен 30. Угол МВО равен разности половины угла АВС и угла АВМ - получаем тоже 30. Следовательно, тр. ВОМ - равнобедренный. Теперь проводим отрезок СК через точку О. Тр.АОС - равнобедренный. Следовательно, угол ОСА = ОАС, а последний легко вычисляется из начальных данных и равен 30. Т.о. угол КВО = DCO, ибо оба по 30, и у нас есть два равных угла в треугольниках КВО и DCO. Заметим теперь вертикальные углы КОВ и DOC и сделаем вывод, что вышеупомянутые треугольники подобны. Но тогда угол ВКО - прямой (ибо равен углу CDO), и отрезок ОК является высотой в равнобедренном тр.ВОМ и, следовательно, серединным перпендикуляром к ВМ. Но точка С лежит на его продолжении, и следовательно ВС=МС. Вот мы и выводим, что тр.ВСМ - равнобедренный! Далее все просто.. Может, не самая изящная задача, но у нее есть вполне определенный смысл. Смысл в том, иногда "случайные" совпадения весьма важны для решения. И если найти зацепку (в данном случае - равенство углов КВО и OCD), то жизнь становится не так и плоха.. Лена - удачи вам и новых встреч! PS Хороший чертеж может и навредить, если быть не очень внимательным. В нашем случае угол КВО иожно принять прямым априори, хотя этот факт нуждается в доказательстве. Сообщение отредактировано: lapp - Эскизы прикрепленных изображений 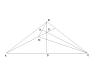
-------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
Сообщений в этой теме
 Лена Помогите решить задачу по геометрии 15.04.2005 2:05
Лена Помогите решить задачу по геометрии 15.04.2005 2:05
 Altair Что за бред?
смотри рисунок....
Если Bесть, то MB… 15.04.2005 2:18
Altair Что за бред?
смотри рисунок....
Если Bесть, то MB… 15.04.2005 2:18

 -никита-
Что за бред?
смотри рисунок....
Если Bесть, то M… 21.11.2016 23:19
-никита-
Что за бред?
смотри рисунок....
Если Bесть, то M… 21.11.2016 23:19
 лена А можно поподробнее для нашей учительницы. 15.04.2005 2:33
лена А можно поподробнее для нашей учительницы. 15.04.2005 2:33
 лена Да наверно ты не понял нужно найти угол ВМС а то ч… 15.04.2005 2:36
лена Да наверно ты не понял нужно найти угол ВМС а то ч… 15.04.2005 2:36
 Altair ТОже просто.
MBC=80, так?
MAB=10
BMC=ACB-MCB,
a… 15.04.2005 2:42
Altair ТОже просто.
MBC=80, так?
MAB=10
BMC=ACB-MCB,
a… 15.04.2005 2:42
 Altair да ипотом вся ясно, верно?
сумма 180, MBC сзнаем и… 15.04.2005 2:46
Altair да ипотом вся ясно, верно?
сумма 180, MBC сзнаем и… 15.04.2005 2:46
 лена Все равно не получается если мы знаем что АВС=100 … 15.04.2005 2:58
лена Все равно не получается если мы знаем что АВС=100 … 15.04.2005 2:58
 лена Олег ну что поможешь???? 15.04.2005 3:16
лена Олег ну что поможешь???? 15.04.2005 3:16
 Лена Все жду помощи, параллельно листаю сборники задач.… 15.04.2005 4:54
Лена Все жду помощи, параллельно листаю сборники задач.… 15.04.2005 4:54
 volvo Лена, можно я попробую вместо Олега? Ты будешь сме… 15.04.2005 5:30
volvo Лена, можно я попробую вместо Олега? Ты будешь сме… 15.04.2005 5:30

 лена Я не смеюсь, т.к. этот несчастный угол я измерила … 15.04.2005 5:44
лена Я не смеюсь, т.к. этот несчастный угол я измерила … 15.04.2005 5:44

 Лена Ещё этот несчастный угол можно н-ти, если доказать… 15.04.2005 5:56
Лена Ещё этот несчастный угол можно н-ти, если доказать… 15.04.2005 5:56
 volvo Вот так это решается (может быть можно конечно и п… 15.04.2005 5:54
volvo Вот так это решается (может быть можно конечно и п… 15.04.2005 5:54
 Лена В 7 классе общеобразовательной школы теоремы синус… 15.04.2005 6:00
Лена В 7 классе общеобразовательной школы теоремы синус… 15.04.2005 6:00
 volvo Лена, я просто давно закончил 7-ой класс, и уже не… 15.04.2005 6:06
volvo Лена, я просто давно закончил 7-ой класс, и уже не… 15.04.2005 6:06
 Лена Если честно, то дочь, примерно с полчаса назад при… 15.04.2005 6:17
Лена Если честно, то дочь, примерно с полчаса назад при… 15.04.2005 6:17
 Лена Я проснулась, но во сне решение не пришло. Взросл… 15.04.2005 6:58
Лена Я проснулась, но во сне решение не пришло. Взросл… 15.04.2005 6:58
 Лена Как же ты всё-таки решаешься, задача? 15.04.2005 7:53
Лена Как же ты всё-таки решаешься, задача? 15.04.2005 7:53
 Лена Короче, училка сказала, что эта задачка решается ч… 15.04.2005 22:30
Лена Короче, училка сказала, что эта задачка решается ч… 15.04.2005 22:30
 Atos Массаракш! Какая-то заколдованная задача :fire… 16.04.2005 9:25
Atos Массаракш! Какая-то заколдованная задача :fire… 16.04.2005 9:25
 Лена В результате мучительных решений за сегодняшнюю но… 16.04.2005 14:52
Лена В результате мучительных решений за сегодняшнюю но… 16.04.2005 14:52
 Лена Я все о задаче.. :low:
Если провести дополнитель… 16.04.2005 21:11
Лена Я все о задаче.. :low:
Если провести дополнитель… 16.04.2005 21:11
 TONIK Лена посмотри мое решение, прилагается к сообщению… 23.04.2005 2:08
TONIK Лена посмотри мое решение, прилагается к сообщению… 23.04.2005 2:08
 TONIK Сорри, лучше по лучше отправлю :D
TONIK, вместо … 23.04.2005 11:20
TONIK Сорри, лучше по лучше отправлю :D
TONIK, вместо … 23.04.2005 11:20
 Legolas Как извесно, сумма углов любого тр-ка равна 180 гр… 18.05.2005 5:26
Legolas Как извесно, сумма углов любого тр-ка равна 180 гр… 18.05.2005 5:26
 Atos Не-а... В том то и дело, что не найдём, так как си… 18.05.2005 11:57
Atos Не-а... В том то и дело, что не найдём, так как си… 18.05.2005 11:57
 -Игорь- Спасибо 1.04.2017 12:19
-Игорь- Спасибо 1.04.2017 12:19  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | 24.02.2026 19:31 |
Связь с администрацией: bu_gen в домене octagram.name








