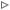uses crt;
const
nn = 10;
type
Matrix = array[1..NN,1..NN+1] of real;
(* построчный ввод матрицы *)
Procedure ReadMatr(var A:Matrix; var n:word );
var
i, j, m: word;
begin
repeat
write('Введите количество линейных уравн. в системе: '); readln(N)
until (N>0) and (N<=NN);
m:=n+1;
For i:=1 to n do begin
For j:=1 to m do begin
write('A[',i,j,']= '); readln(A[i,j])
end
end
end;
(* построчный вывод матрицы *)
Procedure PrintMatr(A:Matrix; n:word);
Var
i, j, m: word;
begin
m:=n+1;
For i:=1 to n do begin
For j:=1 to m do write(A[i,j],' ');
writeln
end
end;
procedure GaussM(a:matrix;n:word; var s:byte; var x:array of real);
var
i, k, j: byte;
m, t: real;
begin
i:=1;
s:=1;
repeat
j:=i+1;
k:=i;
m:=abs(a[i,i]);
repeat
if m<abs(a[j,i]) then begin
m:=abs(a[j,i]);
k:=j;
end;
j:=j+1
until not(j<=n);
if m<>0 then begin
j:=i;
repeat
t:=a[i,j];
a[i,j]:=a[k,j];
a[k,j]:=t;
j:=j+1
until not(j<=n+1);
k:=i+1;
repeat
t:=a[k,i]/a[i,i];
a[k,i]:=0;
j:=i+1;
repeat
a[k,j]:=a[k,j]-t*a[i,j];
j:=j+1
until not(j<=n+1);
k:=k+1
until not(k<=n);
end
else begin
s:=0;
end;
i:=i+1
until not((i<=n)and(s=1));
if s=1 then begin
i:=n;
repeat
x[i]:=a[i,n+1];
j:=i+1;
while j<=n do begin
x[i]:=x[i]-a[i,j]*x[j];
j:=j+1;
end;
x[i]:=x[i]/a[i,i];
i:=i-1
until not(i>=1);
end;
end;
var
b: array[0..nn] of real;
a: Matrix;
n, j: word;
s: byte;
Begin
readmatr(a,n);
printmatr(a,n);
writeln('press any key'); readkey;
GaussM(a,n,s,b);
for j:=1 to n do write (b[j],' ');
writeln('press any key for exit ...'); readkey
end.
 Внимание! Действует предмодерация
Внимание! Действует предмодерация
Подраздел FAQ (ЧАВО, ЧАстые ВОпросы) предназначен для размещения готовых рабочих программ, реализаций алгоритмов. Это нечто вроде справочника, он наполнялся в течение 2000х годов. Ваши вопросы, особенно просьбы решить задачу, не пройдут предмодерацию. Те, кто наполнял раздел, уже не заходят на форум, а с теми, кто на форуме сейчас, лучше начинать общение в других разделах. В частности, решение задач — здесь.
  |
| Altair |

Сообщение
#1
|
 Ищущий истину       Группа: Пользователи Сообщений: 4 825 Пол: Мужской Реальное имя: Олег Репутация:  45 45  |
Решение систем линейных уравнений методом Гаусса
-------------------- Помогая друг другу, мы справимся с любыми трудностями!
"Не опускать крылья!" (С) |
| volvo |

Сообщение
#2
|
|
Гость |
Численное решение систем линейных уравнений методом Зейделя
Const
n = 4; { Порядок системы уравнений }
m = 200; { Допустимое число итераций }
Type
row = Array [1 .. n] Of real;
matrix = Array[1 .. n] Of row;
{ Исходные данные: матрицы A и B (свободные члены) }
Const
A: matrix =
((8, 5, -3, 4),
(2, 2, -1, 1),
(3, 3, -2, 2),
(4, 3, -1, 2));
{
((24, -2, 2, 1),
(-1, 21, 2, -1),
(1, 2, 28, -2),
(0, 1, -2, 20));
}
B: row =
(-8, 6, -2, -4);
{
(54, -61, 28, -45);
}
Var
X: row; { Вектор решения для текущей итерации }
i, j: word;
S, Tolerance: real;
Procedure Seidel(Var A: matrix; Var B, X: row; n, m: word;
Tolerance: real);
Var
Y: row; { Вектор решения для предыдущей итерации }
T: real;
i, j, l: word;
Tolerance_stop_flag: boolean;
Const
k: word = 0;
Iteration_stop_flag: boolean = false;
Begin
For i := 1 To n Do Begin
Y[i] := 0; X[i] := 0
End;
Repeat
k := k + 1;
For i := 1 To n Do Begin
If A[i, i] = 0 Then Begin
l := i;
Repeat
l := l + 1;
If (A[l, i] = 0) and (l = n) Then Begin
WriteLn('Mistake of reduction of system for ', i, 'equation!'); Halt
End
Until A[l, i] <> 0;
T := B[i]; B[i] := B[l]; B[l] := T;
For j := 1 To n Do Begin
T := A[i, j]; A[i, j] := A[l, j]; A[l, j] := T
End;
WriteLn(i, 'and ', l, ' equations of system are rearranged !')
End;
S := 0;
For j := 1 To n Do
If j <> i Then S := S + A[i, j] * X[j];
X[i] := (B[i] - S) / A[i, i]
End;
i := 1;
Tolerance_stop_flag := False;
Repeat
If Abs(X[i] - Y[i]) > Tolerance
Then Tolerance_stop_flag := True
Else i := i + 1
Until (i = n) or Tolerance_stop_flag;
If not Tolerance_stop_flag Then Begin
Iteration_stop_flag := True;
Writeln('Number of iterations: ', k)
End
Else
For i := 1 To n Do Y[i] := X[i]
Until (k = m) or Iteration_stop_flag;
If not Iteration_stop_flag Then
WriteLn('The given number of iterations achieved! ', m)
End; {Seidel}
begin
WriteLn('Метод Зейделя'); WriteLn('A', 'B': 22);
For i := 1 To n Do Begin
For j := 1 To n Do Write(A[i, j]:4:0);
WriteLn(B[i]:10:0)
End;
Repeat
Write('Допустимая точность решения? '); ReadLn(Tolerance)
Until (Tolerance > 0) and (Tolerance < 1);
Seidel(A, B, X, n, m, Tolerance);
WriteLn('Result vector X ', 'Error B-AX': 25);
For i := 1 To n Do Begin
S := 0;
For j := 1 To n Do
S := S + A[i, j] * X[j];
WriteLn(X[i]:15:8, '':13, (B[i]-S):15:8)
End;
ReadLn
end.
|
| volvo |

Сообщение
#3
|
|
Гость |
Решение систем линейных уравнений методом Крамера
Позволяет решить неоднородную систему n линейных алгебраических уравнений с n неизвестными, если определитель основной матрицы не равен нулю. {$N+}
{ Задаем порядок системы уравнений }
Const n = 3;
Type
{ Тип, описывающий матрицу системы (включая свободные члены !!!) }
Equation = Array[1 .. n, 1 .. Succ(n)] Of Double;
matrix =
Array[1 .. n, 1 .. n] Of Double;
Const
a: Equation =
((2, 1, 3, 9),
(1, -2, 1, -2),
(3, 2, 2, 7));
{ Процедура замены очередного столбца матрицы на свободные члены }
Procedure GetMatrix(wout: Integer; Var m: matrix);
Var i, j: Integer;
Begin
For i := 1 To n Do
For j := 1 To n Do
If j <> wout Then m[i, j] := a[i, j]
Else m[i, j] := a[i, Succ(n)]
End;
{ Нахождение определителя }
function det(var p; const size: integer): double;
function minusOne (n : integer): integer;
begin
minusOne := (1 - 2 * Byte (Odd (n)));
end;
function get_addr(i, j : integer;
const n: integer) : integer;
begin
get_addr := pred (i) * n + j
end;
type vector = array[1 .. n * n] of double;
var
my_p : vector absolute p;
pp : ^vector;
s : double;
i, j, curr: integer;
begin
s := 0.0;
if size = 2 then
begin
det := my_p[1]*my_p[4] - my_p[2]*my_p[3]; exit
end;
for i := 1 to size do
begin
GetMem (pp, Sqr (pred (size)) * sizeof (double));
curr := 1;
for j := 1 to size do
if j <> i then
begin
move (my_p[get_addr (j, 2, size)],
pp^[get_addr (curr, 1, pred (size))],
pred(size) * sizeof(double));
inc (curr);
end;
s := s + minusOne (succ(i)) * my_p[get_addr (i, 1, size)] *
det(pp^, pred (size));
FreeMem (pp, Sqr (pred (size)) * sizeof (double))
end;
det := s
end;
Var
i: Integer;
mx: matrix;
Determ: Double;
begin
GetMatrix(Succ(n), mx);
Determ := Det(mx, n);
If Abs(Determ) < 1E-6 Then
Writeln( 'Определитель исходной матрицы = 0' )
Else
For i := 1 To n Do
Begin
GetMatrix(i, mx);
WriteLn( 'x(', i, ') = ', (Det(mx, n) / Determ):7:4 )
End
end.
|
| hiv |

Сообщение
#4
|
|
Профи     Группа: Пользователи Сообщений: 660 Пол: Мужской Реальное имя: Михаил Репутация:  11 11  |
Решение системы линейных уравнений методом Холецкого
Этот метод менее подвержен накопительным ошибкам в сравнении с методом Гаусса. Поэтому им можно решать системы из многих десятков уравнений! Код program HOLETSKY; {$M 65520, 65520, 65520} const max_eq = 50; type RealType=double; MCvector = array [0..max_eq] of RealType; {вектор} MCmatr = array [0..max_eq,0..max_eq] of RealType; {запись типа матрица} function maxval(x,y:realtype):realtype; begin if x<y then maxval:=y else maxval:=x; end; procedure Holetskiy(N:integer;A0:MCmatr; B0:MCvector; var X:MCvector; var error:RealType); var i,j,m,k,p :byte; s,e,max :RealType; A :MCmatr; begin if (N>max_eq)or(N<2) then begin writeln('Ошибка в передаваемых данных.'); halt(1); end; A:=A0; for i:=0 to N-1 do A[i,N]:=B0[i]; for i:=0 to N-1 do {выбор главного элемента по диагонали} begin max:=0; for j:=i to N-1 do if max<abs(A[i,j]) then begin max:=abs(A[i,j]); p:=j; end; if p<>i then begin for j:=0 to N do A[N,j]:=A[i,j]; for j:=0 to N do A[i,j]:=A[p,j]; for j:=0 to N do A[p,j]:=A[N,j]; end; end; {метoд хoлецкoгo} for j:=1 to N do A[0,j]:=A[0,j]/A[0,0]; for m:=1 to N-1 do begin for i:=m to N-1 do begin s:=0; for k:=0 to m-1 do s:=s+A[i,k]*A[k,m]; A[i,m]:=A[i,m]-s end; for j:=m+1 to N do begin s:=0; for k:=0 to m-1 do s:=s+A[m,k]*A[k,j]; A[m,j]:=(A[m,j]-s)/A[m,m] end; end; X[N-1]:=A[N-1,N]; for i:=N-2 downto 0 do begin s:=0; for k:=i+1 to N-1 do s:=s+A[i,k]*X[k]; X[i]:=A[i,N]-s end; {расчет ошибки} error:=0; for i:=0 to N-1 do begin s:=0; for j:=0 to N-1 do if i=j then s:=s+(A0[i,j]+1)*X[j] else s:=s+A0[i,j]*X[j]; s:=s-B0[i]; error:=maxval(error,abs(X[i]-s)); end; end; var A :MCmatr; B,X :MCvector; err :RealType; n,i,j :integer; begin {of program} writeln('Решение системы линейных уравнений метoдoм Хoлецкoгo'); writeln('с выбoрoм главнoгo элемента.'); write('Введите числo уравнений = ');read(N); for i:=0 to N-1 do begin writeln('Введите кoэффициенты ',i:0,'-го уравнения:'); for j:=0 to N-1 do begin write('A[',i:0,',',j:0,'] = '); readln(A[i,j]); end; write('B[',i:0,'] = '); readln(B[i]); end; Holetskiy(N,A,B,X,err); writeln('Решение уравнения:'); for i:=0 to N-1 do writeln('X[',i:0,'] = ',X[i]); writeln('Точность резутьтата =',err); end. -------------------- Никогда не жадничай. Свои проблемы с любовью дари людям!
|
  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | 18.04.2025 0:32 |
Связь с администрацией: bu_gen в домене octagram.name