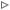1) Упростить: (9x^(-4)-4x^(-2)+4x^(-1)-1)/(3x^(-3)-2x^(-2)+x^(-1))
2) Вычеслить tgx, если 4cos(2x)+5sin(2x)=2sin^(2)(x), x- угол 3 четверти.
 Компиляция правил для данного раздела
Компиляция правил для данного раздела
1. Заголовок темы должен быть информативным. В противном случае тема закрывается и удаляется ...
2. НЕ используйте форум для личного общения, все что не относится к обсуждению темы - на PM!
3. Одна тема - один вопрос (задача)
4. Спрашивайте и отвечайте четко и по существу!!!
  |
| Crowen |

Сообщение
#1
|
|
Группа: Пользователи Сообщений: 4 Пол: Мужской Реальное имя: Пётр Репутация:  0 0  |
|
| zZz |

Сообщение
#2
|
 Пионер   Группа: Пользователи Сообщений: 55 Пол: Мужской Реальное имя: Алексей Репутация:  0 0  |
|
| Clerick |

Сообщение
#3
|
 студент..    Группа: Пользователи Сообщений: 287 Пол: Мужской Реальное имя: Дмитрий Репутация:  2 2  |
2) Вычеслить tgx, если 4cos(2x)+5sin(2x)=2sin^(2)(x), x- угол 3 четверти. Используй формулы выражения sin2x через tg половинного аргумента sin2x= 2tgx/(1+tg^(2)(x)) и соотвественно cos2x=(1-tg^(2)(x))/(1+tg^(2)(x)) Подставляем их, преобразовываем знаменатель 1+tg^(2)(x)=1+Sin^(2)(x)/cos^(2)(x)=1/cos^(2)(x) т.е. получаем 5*2tgx*cos^(2)(x)+4(1-tg^(2)(x))*cos^(2)(x)=2sin^(2)(x) Делим на cos^(2)(x) (число не равное нулю поэтому и делим, в противном случае, если считать, что cosx=0, то уравнение решении не имеет) и решаем квардратное уравнение относительно искомого tgx с учетом того что угол x 3 четверти(при выборе ответа отталкиваемся от того, что tgx>0). Вроде так, если я ни где не ошибся. Сообщение отредактировано: Clerick - -------------------- После дождя обязательно выглянет солнце)
|
  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | 5.04.2025 14:36 |
Связь с администрацией: bu_gen в домене octagram.name