Всем Доброго времени суток. Что то ни как не могу решить эту задачку.
В прямоугольном треугольнике АВС угол С = 90, медианы СС1 и ВВ1 перпендикулярны, найти длинны этих медиан, если медиана АА1 =3(SQRT(3)) (три корня из трех).
Заранее благодарен.
 Компиляция правил для данного раздела
Компиляция правил для данного раздела
1. Заголовок темы должен быть информативным. В противном случае тема закрывается и удаляется ...
2. НЕ используйте форум для личного общения, все что не относится к обсуждению темы - на PM!
3. Одна тема - один вопрос (задача)
4. Спрашивайте и отвечайте четко и по существу!!!
  |
| al6262 |

Сообщение
#1
|
|
Новичок  Группа: Пользователи Сообщений: 11 Пол: Мужской Реальное имя: Алексей Репутация:  0 0  |
|
| Michael_Rybak |

Сообщение
#2
|
|
Michael_Rybak      Группа: Пользователи Сообщений: 1 046 Пол: Мужской Реальное имя: Michael_Rybak Репутация:  32 32  |
Пусть О - точка пересечения медиан.
По условию, угол ВОС = 90 Поскольку СС1 - медиана, треугольник СС1В - равнобедренный, и улгы С1СВ и СВС1 равны Поэтому трегуольники ВОС и АСВ подобны, а именно: BC = OC * k AC = OВ * k AB = BC * k Где k - коэф. подобия. Найдем k. Запишем площадь трапеции СВС1В1. С одной стороны, она равна CC1 * BB1 / 2 (диагонали перпендикулярны) С другой стороны, она равна 3/4 * AC * BC / 2 (треугольники СС1В1, СС1А1, А1С1В и АВ1С1 равны). Имеем: CC1 * BB1 / 2 = 3/4 * AC * BC / 2 Поскольку О - точка пересечения медиан, имеем CC1 = 3/2 * CO, BB1 = 3/2 * BO Также помним, что BC = OC * k и АC = OВ * k Подставим: CC1 * BB1 / 2 = 3/4 * AC * BC / 2 3/2 * CO * 3/2 * BO / 2 = 3/4 * OB * k * OC * k / 2 3 = k*k Поэтому коэф. подобия равен SQRT(3). Поскольку О - точка пересечения медиан, имеем OA1 = 1/3 * AA1 = SQRT(3). ОА1 - медиана в прямоугольном треугольнике СОВ, поэтому ВС = 2ОА1 = 2 * SQRT(3). AB = BC * k = 2 * SQRT(3) * SQRT(3) = 6 AC = SQRT(6*6 - 3) = SQRT(33) BB1 = 3/2 * OB = 3/2 * AC / k = 3/2*SQRT(11) CC1 = 3/2 * OC = 3/2 * CB / k = 3 Ответы не особо красивые вышли, мог ошибиться в вычислениях, да и само решение, похоже, излишне громоздко. Ну что ж |
| Lapp |

Сообщение
#3
|
 Уникум        Группа: Пользователи Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
Ответы не особо красивые вышли, мог ошибиться в вычислениях, да и само решение, похоже, излишне громоздко. Да нет, все ничего. Может, только привлечение площади было излишне.. 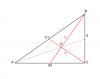 Из подобия можно сказать, что y = k*a/2 (медиана в большом прямоугольном треугольнике). Тоже из подобия можно сказать k*(2/3)*y = a . Это дает простенькую системку (выражаем у из одного, подставляем в другое, "а" выпадает совсем), из которой следует k = Sqrt(3) - в точности как у тебя. И сразу, зная а (те же рассуждения, что и у тебя, не привожу), имеем y из первой приведенной мной формулы. х можно найти, например, с помощью теоремы Пифагора. Единственное замечание: чертежик все же имеет смысл приводить.. Я обычно использую тривиальный Paint, который входит в Винду, и сейвлю в формат GIF - так получается наиболее экономно для таких целей.. -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
| al6262 |

Сообщение
#4
|
|
Новичок  Группа: Пользователи Сообщений: 11 Пол: Мужской Реальное имя: Алексей Репутация:  0 0  |
Огромное спасибо.
И еще один вопросик, вернее задачка. Время поджимает, решить не успеваю. Дан квадрат ABCD. На АВ лежит точка К, на стороне ВС точка L, на стороне CD точка М. Четырехугольник AKLM равнобокая трапеция. Найти основания трапеции, если АК = 5 и MD =2. Заранее благодарен. Сообщение отредактировано: al6262 - |
| Lapp |

Сообщение
#5
|
 Уникум        Группа: Пользователи Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
И еще один вопросик, вернее задачка. В следующий раз новую задачу пость в новую тему. Время поджимает, решить не успеваю. Постарайся не приводить свои личные трудности в качестве оправданий. Оправдания тут никого не интересуют (тут не завучи), а твои слова трактуются как явный намек, что ты человек занятый, а мы все тут - лоботрясы. И у вас-то уж, мол, времени навалом - а я бы уж конечно решил бы, если бы было время... Извини за нескромный вопрос - и сколько тебе нужно времени на такую задачу?.. Оно нормировано? Типа как нормо-часы выкопать яму?.. Ладно, извини за нравоучения - надеюсь, они на пользу.. Решение получается из составления системы уравнений. Система получается из подобия KBL и MDA, теоремы Пифагора для LCM и того условия, что все стороны квадрата равны.. Если этого не хватит - приходи за остальным. -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
| al6262 |

Сообщение
#6
|
|
Новичок  Группа: Пользователи Сообщений: 11 Пол: Мужской Реальное имя: Алексей Репутация:  0 0  |
2 lapp. Ок, замечания учту на будующее. Блогодоря твоему совету разобрался, спасибо за помощь.
|
| Lapp |

Сообщение
#7
|
 Уникум        Группа: Пользователи Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
-------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | 18.02.2026 19:30 |
Связь с администрацией: bu_gen в домене octagram.name









