"Даны координаты вершин треугольника и окружность, заданная уравнением x^2+y^2=r^2. Определить, является ли окружность вписанной или описанной по отношению к треугольнику."
Помогите ришить пожалуйста.
1. Заголовок темы должен быть информативным. В противном случае тема удаляется ...
2. Все тексты программ должны помещаться в теги [code=pas] ... [/code], либо быть опубликованы на нашем PasteBin в режиме вечного хранения.
3. Прежде чем задавать вопрос, см. "FAQ", если там не нашли ответа, воспользуйтесь ПОИСКОМ, возможно такую задачу уже решали!
4. Не предлагайте свои решения на других языках, кроме Паскаля (исключение - только с согласия модератора).
5. НЕ используйте форум для личного общения, все что не относится к обсуждению темы - на PM!
6. Одна тема - один вопрос (задача)
7. Проверяйте программы перед тем, как разместить их на форуме!!!
8. Спрашивайте и отвечайте четко и по существу!!!
| SataNi |

Сообщение
#1
|
|
Новичок  Группа: Пользователи Сообщений: 15 Пол: Мужской Репутация:  0 0  |
Такая вот задачка:
"Даны координаты вершин треугольника и окружность, заданная уравнением x^2+y^2=r^2. Определить, является ли окружность вписанной или описанной по отношению к треугольнику." Помогите ришить пожалуйста. |
  |
| Lapp |

Сообщение
#2
|
 Уникум        Группа: Пользователи Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
Такая вот задачка: окружность, заданная уравнением x^2+y^2=r^2. Окружность на самом деле с центром в начале координат, или ты имеешь в виду что известен только радиус, а не центр? -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
| volvo |

Сообщение
#3
|
|
Гость |
Где копать? Пожалуйста... Копай сюда: если окружность описанная, то все вершины лежат на окружности (у тебя есть координаты вершин и уравнение окружности, проверяй
Необходимые формулы можешь посмотреть на АлгоЛисте |
| SataNi |

Сообщение
#4
|
|
Новичок  Группа: Пользователи Сообщений: 15 Пол: Мужской Репутация:  0 0  |
lapp, про то что у неё центр в начале координат ничего не сказано
volvo, сорри, я новенький на форуме... |
| Lapp |

Сообщение
#5
|
 Уникум        Группа: Пользователи Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
про то что у неё центр в начале координат ничего не сказано ... я новенький на форуме... То, что ее уравнение задано в такой форме, это и есть сказано. Именно это и удивляет, так как такое условие в принципе кажется лишним и, скорее всего, противоречивым. Уравнение окружности действительно присутствовало в условии или это ты дописал? форум тут ни при чем. Берешь Яндекс и ищешь: АлгоЛист.. -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
| SataNi |

Сообщение
#6
|
|
Новичок  Группа: Пользователи Сообщений: 15 Пол: Мужской Репутация:  0 0  |
Текст задания точный. Книга передо мной лежит...
Цитата форум тут ни при чем. Берешь Яндекс и ищешь: АлгоЛист.. Пасиб! |
| Lapp |

Сообщение
#7
|
 Уникум        Группа: Пользователи Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
Текст задания точный. Книга передо мной лежит... Тоды ой.. Не знаю, как это будет вязаться с реальными координатами точек, но проверка тогда явно облегчается: нужно всего лишь проверить для вершин треугольника равенство x^2+y^2=r^2 Только меня все же гложут сомнения... Дествительно условие точное и полное? -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
| SataNi |

Сообщение
#8
|
|
Новичок  Группа: Пользователи Сообщений: 15 Пол: Мужской Репутация:  0 0  |
Точно полное и точно точное
Ладно завтра подумаю ещё... Сегодня уже не думается |
| Lapp |

Сообщение
#9
|
 Уникум        Группа: Пользователи Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
Если хочеш сфотать могу Я тебе верю.. Но тогда решение с одной стороны упрощается, с другой - в большинстве случаев просто невозможно. То есть надо, чтоб випсанная или описанная окружность треугольника была центрирована на начало координат. -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
| Гость |

Сообщение
#10
|
|
Гость |
Млин... Не получается чтото... Напишите, пожалуйста, хотя бы примерный код
|
| Lapp |

Сообщение
#11
|
 Уникум        Группа: Пользователи Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
Млин... Не получается чтото... Напишите, пожалуйста, хотя бы примерный код Ты покажи, что именно получается и что не получается. Мы подправим.. -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
| SataNi |

Сообщение
#12
|
|
Новичок  Группа: Пользователи Сообщений: 15 Пол: Мужской Репутация:  0 0  |
Получилось чтото вроде этого:
Program laba2; Не знаю правильно или нет... Но вродебы правильно |
| Lapp |

Сообщение
#13
|
 Уникум        Группа: Пользователи Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
1. Почему ты рассчитываешь радиус окружности так:
r:=SQRT(SQR(o1)+SQR(o2)); ? Получается, что твоя окружность обязательно проходит через начало координат. Мне кажется, разумнее запрашивать радиус, как ты запрашиваешь все остальное. Хотя, я вообще не понимаю, как это вяжется с условием, в котором центр окружности железно помещен в начало координат.. 2. Проверку на равенство двух переменных типа real (и подобных) нельзя проводить простым равенством. Дело в том, что из-за неизбежных ошибок вычисления два равных числа могут реально оказаться неравными в машинном представлении. Нужно сравнивать разность чисел с подходящим маленьким числом, например: Abs(a-b)<1e-7 Это число выбирается из соображений длины представления используемого типа и порядка чисел. -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
| SataNi |

Сообщение
#14
|
|
Новичок  Группа: Пользователи Сообщений: 15 Пол: Мужской Репутация:  0 0  |
1. Почему ты рассчитываешь радиус окружности так: r:=SQRT(SQR(o1)+SQR(o2)); ? Получается, что твоя окружность обязательно проходит через начало координат. Почему? Не проходит она обязательно через начало координат... Так я рассчитываю, потому что окружность задана таким уравнением... Просто по введённым координатам программа рассчитывает радиус, формула которого записана в условии... Разве неправильно? 2. Проверку на равенство двух переменных типа real (и подобных) нельзя проводить простым равенством. Это лаборатрная по теме разветвляющиеся алгоритмы, 3я по счёту.. Думаю преподам пофиг будет на это... Лишь бы алгоритм верный был... |
| Lapp |

Сообщение
#15
|
 Уникум        Группа: Пользователи Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
Почему? Не проходит она обязательно через начало координат... Так я рассчитываю, потому что окружность задана таким уравнением... Просто по введённым координатам программа рассчитывает радиус, формула которого записана в условии... Разве неправильно? Смотри рисунок. Это то, что ты делаешь. 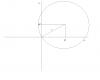 В условии было x^2+y^2=r^2, то есть окружность с центром в начале координат. Боюсь, ты путаешь координаты точки на окружности (х,у) и координаты ее центра (о1,о2) Это лаборатрная по теме разветвляющиеся алгоритмы, 3я по счёту.. Думаю преподам пофиг будет на это... Лишь бы алгоритм верный был... Ну-ну.. хотя бы знай, что ответить, если спросят.. -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
| Volvo (guest) |

Сообщение
#16
|
|
Гость |
Цитата Думаю преподам пофиг будет на это... Лишь бы алгоритм верный был... "Преподы", как ты их называешь, сначала запустят программу, и если программа выдаст неверный результат (а при таком сравнении - вероятность велика), то они даже не посмотрят на твой алгоритм, потому что программа в первую очередь должна выдавать правильный ответ, а уж потом делать это красиво, быстро, и т.д. |
| SataNi |

Сообщение
#17
|
|
Новичок  Группа: Пользователи Сообщений: 15 Пол: Мужской Репутация:  0 0  |
До меня не дойдёт почему у окружности центр - начало координат? В условии этого не сказано...
|
| Lapp |

Сообщение
#18
|
 Уникум        Группа: Пользователи Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
До меня не дойдёт почему у окружности центр - начало координат? В условии этого не сказано... Общее уравнение окружности такое: (x-Xc)^2 + (y-Yc)^2 = r^2 где Xc, Yc - координаты центра окружности. У тебя в условии уравнение такое: x^2+y^2=r^2 Что можно переписать так: (x-0)^2 + (y-0)^2=r^2 Теперь сравни это с общим уравнением. Видишь? Xc и Yc равны нулю.. Ясно? -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
| SataNi |

Сообщение
#19
|
|
Новичок  Группа: Пользователи Сообщений: 15 Пол: Мужской Репутация:  0 0  |
Теперь ясно... То есть получается, что координаты центра окружности известны(начало координат) и надо сделать ввод с клавы радиуса... Только на кой хрен мне тогда нужны x и y? Зачем мне эта точка на окружности?
PS: Сорри что туплю |
| Lapp |

Сообщение
#20
|
 Уникум        Группа: Пользователи Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
Только на кой хрен мне тогда нужны x и y? Зачем мне эта точка на окружности? Ты про какие x и y? Которые входят в уравнение? Они представляют произвольную точку на кривой (в данном случае - окружности). Как же без них записать уравнение?.. Ты прав, тебе нужно вводить только радиус. И проверять лежат ли вершины треугольника на этой укружности (то есть удовлетворяют ли их координаты ур-ию окружности) - это для случая описанной окружности - либо делать проверку для вписанной (скажем, как ты делал). Теперь понятнее? -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
  |

|
Текстовая версия | 17.02.2026 17:26 |