 Прочтите прежде чем задавать вопрос!
Прочтите прежде чем задавать вопрос!
1. Заголовок темы должен быть информативным. В противном случае тема удаляется ...
2. Все тексты программ должны помещаться в теги [code=pas] ... [/code], либо быть опубликованы на нашем PasteBin в режиме вечного хранения.
3. Прежде чем задавать вопрос, см. "FAQ", если там не нашли ответа, воспользуйтесь ПОИСКОМ, возможно такую задачу уже решали!
4. Не предлагайте свои решения на других языках, кроме Паскаля (исключение - только с согласия модератора).
5. НЕ используйте форум для личного общения, все что не относится к обсуждению темы - на PM!
6. Одна тема - один вопрос (задача)
7. Проверяйте программы перед тем, как разместить их на форуме!!!
8. Спрашивайте и отвечайте четко и по существу!!!
  |
| Vasya! |

Сообщение
#1
|
|
Новичок  Группа: Пользователи Сообщений: 35 Пол: Мужской Реальное имя: Вася Репутация:  0 0  |
Говорят, что копьютер вычислял-вычислял и вычислил (например за трое суток) 500 000 000 знаков.
А как вычисляется число Пи? |
| klem4 |

Сообщение
#2
|
 Perl. Just code it!       Группа: Пользователи Сообщений: 4 100 Пол: Мужской Реальное имя: Андрей Репутация:  44 44  |
-------------------- perl -e 'print for (map{chr(hex)}("4861707079204E6577205965617221"=~/(.{2})/g)), "\n";'
|
| Vasya! |

Сообщение
#3
|
|
Новичок  Группа: Пользователи Сообщений: 35 Пол: Мужской Реальное имя: Вася Репутация:  0 0  |
Это я видел. А я бы хотел понять алгоритм нахождения числа (и желательно больше 54 000).
|
| volvo |

Сообщение
#4
|
|
Гость |
Цитата и желательно больше 54 000 Переходи на 32 бита, где длина строки может достигать 2 Gb, и вычисляй сколько нужно знаков... В ДОС-овском Паскале ты ограничен размером сегмента, отсюда и ограничение на число символов... |
| Vasya! |

Сообщение
#5
|
|
Новичок  Группа: Пользователи Сообщений: 35 Пол: Мужской Реальное имя: Вася Репутация:  0 0  |
А как насчет принципа, алгоритма вычисления числа.
|
| volvo |

Сообщение
#6
|
|
Гость |
Я же написал в теме по ссылке, что не имею понятия об алгоритме. Невнимательно читал?
Погугли на тему "BBP - Formula", "Bailey-Borwein-Plouffe Formula"... Что-нибудь да найдется |
| Vasya! |

Сообщение
#7
|
|
Новичок  Группа: Пользователи Сообщений: 35 Пол: Мужской Реальное имя: Вася Репутация:  0 0  |
Спасибо and sorry!!!
|
| Lapp |

Сообщение
#8
|
 Уникум        Группа: Пользователи Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
Алгоритмов существет много разных. Самый простой и понятный - формула Лейбница:
П/4 = 1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + .. Поскольку ряд знакопеременный с убывающим по модулю общим членом, то точность конечной суммы оценивается последним членом. То есть написанный выше кусок даст примерно точность до первого знака после запятой, а если нужно, например, точность до третьего знака, 0.001 (одна тысячная) , то нужно взять сумму, заканчивающуюся членом 1/1001, то есть примерно 500 членов ряда. Извиняюсь в посте была ошибка. Сейчас исправлено (выделено зеленым цветом) Сообщение отредактировано: lapp - -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
| Lapp |

Сообщение
#9
|
 Уникум        Группа: Пользователи Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
Понятно, что формула Лейбница сходится очень медленно. Вот этот ряд сходится гораздо скорее:
П/(2*Sqrt(3) = 1 - (1/3)(1/3) + (1/5)(1/3)^2 - (1/7)(1/3)^3 + (1/9)(1/3)^4 - (1/11)(1/3)^5 + ... Приведенный его фрагмент обеспечивает точность лучше одной сотой, а если добавить еще всего один член, то будет 0.001, на достижение которой с формулой Лейбница уходит 500 членов. -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
| Vasya! |

Сообщение
#10
|
|
Новичок  Группа: Пользователи Сообщений: 35 Пол: Мужской Реальное имя: Вася Репутация:  0 0  |
А если вычислять по формуле Лейбница, то этот процесс понятно, что долгий, но он точный?
|
| Lapp |

Сообщение
#11
|
 Уникум        Группа: Пользователи Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
А если вычислять по формуле Лейбница, то этот процесс понятно, что долгий, но он точный? Я же написал оценку точности! Или ты думаешь, что это теория, которая типа сама по себе, а практика сама по себе?... Повторяю: любой знакопеременный ряд с убывающим по модулю общим членом оценивается следующим образом (в предположении, что An<0, а A(n+1)>0 ) : Sn < S < S(n+1) , где S - бесконечеая сумма. Вычитая из правого неравенства Sn, имеем: S - Sn < S(n+1) - Sn = A(n+1) Поскольку обе стороны положительны, можем поставить модули |S - Sn| < |S(n+1) - Sn| = |A(n+1)| Я не буду доказывать эту формулу для An>0, это практически очевидно. Сказанное можно проиллюстрировать картинкой: 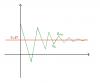 Короче, имеем следующее: Несмотря на то, что мы не знаем бесконечной суммы и не можем ее узнать, мы можем сказать, что всякая n-ная конечная сумма отличается от нее по модулю не более, чем модуль следующего члена ряда. Иначе говоря, если мы знаем, что |An|=0.001, то для того, чтобы получить точность в одну тысячную, нам достаточно сложить n-1 членов ряда. Теперь ясно? -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
| Reflex |

Сообщение
#12
|
 Пионер   Группа: Пользователи Сообщений: 118 Пол: Женский Репутация:  0 0  |
есть еще алгоритм через арктангенсы как-то...
-------------------- Нам не дано предугадать как наше слово отзовется...
|
| Lapp |

Сообщение
#13
|
 Уникум        Группа: Пользователи Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
есть еще алгоритм через арктангенсы как-то... Уважаемая Reflex, да будет тебе известно, что вторая из приведенных мной формул и есть разложение арктангенса в ряд.. -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
| Vasya! |

Сообщение
#14
|
|
Новичок  Группа: Пользователи Сообщений: 35 Пол: Мужской Реальное имя: Вася Репутация:  0 0  |
Огромное спасибо!!! Буду пока разбираться с тем что есть.
Кстати С Днем Рождения!!! |
| Vasya! |

Сообщение
#15
|
|
Новичок  Группа: Пользователи Сообщений: 35 Пол: Мужской Реальное имя: Вася Репутация:  0 0  |
Иначе говоря, если мы знаем, что |An|=0.001, то для того, чтобы получить точность в одну тысячную, нам достаточно сложить n-1 членов ряда.
Вот это не очень ясно! Пример какой-то можешь привести. |
| Lapp |

Сообщение
#16
|
 Уникум        Группа: Пользователи Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
Вот это не очень ясно! Пример какой-то можешь привести. Какой пример?.. Я привел тебе точное математическое доказательство! Да еще и с рисунком!! Дай себе труд всмотреться в график - и ты все поймешь, там нет ничего сложного. Или уж открой любой учебник по матану, найди там тему знакопеременные ряды, прочти доказательство еще раз. А пример - ты, в конце концов его сам и делаешь. Так трудно закодировать несколько строк и убедиться? Код { Calculation the Pi, Liebniz formula } var i,n:integer; s,z:real; begin Write(' N = ');ReadLn(n); s:=0; z:=1; for i:=1 to n-1 do begin s:=s+z*1/(2*i-1); z:=-z end; WriteLn(' An = ',(1/n):10:8); WriteLn(' S(n-1) = ',s:10:8); WriteLn(' Pi/4 = ',(Pi/4):10:8); WriteLn(' 4*S(n-1) = ',(4*s):10:8); WriteLn(' Pi = ',Pi:10:8); ReadLn end. -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | 15.05.2024 0:10 |
Связь с администрацией: bu_gen в домене octagram.name









