Аналитическая геометрия
Please help! Как найти уравнение касательной к окружности, проходящей через заданную точку? И уравнения касательных к двум окружностям
 Компиляция правил для данного раздела
Компиляция правил для данного раздела
1. Заголовок темы должен быть информативным. В противном случае тема закрывается и удаляется ...
2. НЕ используйте форум для личного общения, все что не относится к обсуждению темы - на PM!
3. Одна тема - один вопрос (задача)
4. Спрашивайте и отвечайте четко и по существу!!!
  |
| Master Yoda |

Сообщение
#1
|
|
Группа: Пользователи Сообщений: 6 Пол: Мужской Реальное имя: d Репутация:  0 0  |
|
| Phoenix |

Сообщение
#2
|
|
Группа: Пользователи Сообщений: 8 Пол: Мужской Репутация:  1 1  |
уравнение касательной к окружности в данной точке (мат формула):
( х1 – х0 ) ( х – х0 ) + ( у1 – у 0 ) ( у – у 0 ) = R^2 |
| Master Yoda |

Сообщение
#3
|
|
Группа: Пользователи Сообщений: 6 Пол: Мужской Реальное имя: d Репутация:  0 0  |
|
| Lapp |

Сообщение
#4
|
 Уникум        Группа: Пользователи Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
уравнение касательной к окружности в данной точке (мат формула): ( х1 – х0 ) ( х – х0 ) + ( у1 – у 0 ) ( у – у 0 ) = R^2 Формула неверная. В правой части должен стоять ноль: ( х1 – х0 ) ( х – х0 ) + ( у1 – у 0 ) ( у – у 0 ) = 0 Ну и перменные надо объяснять, если уж даешь формулу. Для полной ясности. x0,y0 - центр окружности, x1,y1 - точка на окружности, через которую проходит касательная. Что касается формулы для касательной через произвольную точку вне окружности... надо подумать! -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
| Lapp |

Сообщение
#5
|
 Уникум        Группа: Пользователи Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
Путь решения может быть примерно таким (см. рис.)
Дано: центр окружности x0,y0, радиус R и точка с координатами a,b в произвольном месте. Найдем угол альфа как arctg((b-y0)/(a-x0)) Дальше найдем угол бета как arccos( R / Sqrt((a-x0)^2+(b-y0)^2) ) Теперь Найдем угол гамма как 2п - альфа - бета И наконец, находим точку x1,y1 вот так: x1=x0-R*cos(гамма) и y1=y0+R*sin(гамма) Когда точка x1,y1 найдена, применяем формулу для касательной через точку на окружности.. Способ тяжеловатый получился.. Эскизы прикрепленных изображений 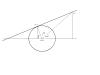
-------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
| none |

Сообщение
#6
|
|
Гость |
Формула неверная. В правой части должен стоять ноль: ( х1 – х0 ) ( х – х0 ) + ( у1 – у 0 ) ( у – у 0 ) = 0 Ну и перменные надо объяснять, если уж даешь формулу. Для полной ясности. x0,y0 - центр окружности, x1,y1 - точка на окружности, через которую проходит касательная. Что касается формулы для касательной через произвольную точку вне окружности... надо подумать! И всетаки ( х1 – х0 ) ( х – х0 ) + ( у1 – у 0 ) ( у – у 0 ) = R^2 http://www.bymath.net/studyguide/angeo/sec/angeo3.htm |
| Lapp |

Сообщение
#7
|
 Уникум        Группа: Пользователи Сообщений: 6 823 Пол: Мужской Реальное имя: Лопáрь (Андрей) Репутация:  159 159  |
И всетаки ( х1 – х0 ) ( х – х0 ) + ( у1 – у 0 ) ( у – у 0 ) = R^2 Да, похоже, что так.. Не знаю, что на меня тогда нашло Извиняюсь. Формула правильная, подтверждаю. Бывает.. помутнения но надеюсь, что решение о касательной все же верное (формула в нем участвует только на последней стадии). Спасибо за исправление! -------------------- я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой |
| -ОЛЯ- |

Сообщение
#8
|
|
Гость |
нашла вот что, уравнение касательной к окружности в произвольной точке M(x0;y0) : xx0+yy0=RR(радиус в квдрате)
|
  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | 14.04.2025 15:17 |
Связь с администрацией: bu_gen в домене octagram.name