Разложение силы, Тангенциальная и радиальная составляющие Опции

[Tony]

Добрый день.

Вот возник следующий вопрос: допустим у нас имеется твердое тело с центром масс в точке О. К некой точке P этого тела приложена сила F (см. рисунок). Требуется разложить эту силу на радиальную и тангенциальную составляющие, т.е. на силу, 'двигающую' данное тело (Fr), и на силу, 'вращающую' его (Ft).



Как я понимаю, вектор радиальной составляющей должен быть направлен из точки О в точку M, a тангенциальной - перпендикулярно OP. При этом в сумме они должны составлять силу F.

Однако попытки применить эти соображения к другим случаям приводят к неудачам:



В этом случае Ft и Fr в сумме не равны F.

Собственно, просьба указать на дыру в моих рассуждениях .

[Lapp]

Требуется разложить эту силу на радиальную и тангенциальную составляющие, т.е. на силу, 'двигающую' данное тело (Fr), и на силу, 'вращающую' его (Ft).
...
Собственно, просьба указать на дыру в моих рассуждениях .

Дыра не в решении, дыра в условии.
Откуда оно? Кто поставил задачу? Разделение силы на "двигающую" и "вращающую" неверно по сути. Сила (нескомпенсированная), приложенная к телу, создает ускорение. Так? С Ньютоном не поспоришь)). Чему равно это ускорение? Правильно , a=F/m. Но твердое тело - не материальная точка, в нем разные точки имеют разные скорости и ускорения. Есть в твердом теле точка, двигающаяся с ускорением a? Да, есть, эта точка - центр масс. Следовательно, на вопрос о том, какая сила является "двигающей" надо отвечать однозначно: полная, то есть F, ни на какие части не разложенная.

Тогда возникает вопрос: но тело вращается? Ответ: вполне возможно. А что его вращает? А вращает его не сила, а момент сил. И это уже совсем другой разговор.

Я могу понять, что двигало автором условия. Скажем, если у нас есть ящик на полу, и нам нужно его оттолкать куда-нить в угол. Как мы будем направлять силу? Естественно, так, чтобы ее линия прошла через ЦМ. А не хватаем за угол и не тянем вбок. Из этого можно сделать вывод, что сила, проходящая церез ЦМ - она как бы двигающая. Следовательно, для того, чтоб ее найти, нужно спроектировать F на прямую (не отрезок) ОР (эта составляющая на первом рисунке будет направлена от ЦМ, а не к нему). А другая составляющая пойдет по перпендикулярной прямой. Если автор задачи имел в виду это и целью является ему угодить - ну, отвечай так. Но только это полнейший бред .

[Tony]

Если честно, никакой задачи нет.

Дело в том, что я пишу программу - физический симулятор (ну симулятор - это громко сказано, пока реализованы только столкновения (удары ) тел, трения нет, гравитации тоже ) на основе метода импульсов. Все это дело происходит на плоскости. Тела - произвольные выпуклые многоугольники.

Движение каждого тела характеризуется проекциями линейной скорости Vx и Vy и угловой скоростью W.

Собственно изменение скоростей - линейной и угловой - под действием сил в течение промежутка времени dt происходит следующим образом:

Vx=Vx + dt * Fx / m

Vy=Vy + dt * Fy / m

W=W + dt * T / I

где M - масса тела, I - момент инерции тела.

Если с линейной скоростью все понятно (если F=ma, то массы сократятся, а ускорение * время как раз и дает прирост скорости), то с угловой не очень...Получается, что T - это аналог F для вращательного движения, но получается, что T - скаляр, и как его назвать? Момент силы? Или нет?

Вот собственно и вопрос - если на произвольную точку тела действует внешняя сила, как она отразится на линейной и угловой скоростях...

P.S. Я - школьник, в программе такого нет (по крайней мере у нас), так что если что не так - просьба не пинать .

[sheka]

Вот возник следующий вопрос: допустим у нас имеется твердое тело с центром масс в точке О. К некой точке P этого тела приложена сила F (см. рисунок). Требуется разложить эту силу на радиальную и тангенциальную составляющие, т.е. на силу, 'двигающую' данное тело (Fr), и на силу, 'вращающую' его (Ft).

Это точно полное и точное условие???
Если да, то на сколько я понял, задача на теорию (знаешь ли ты вообще куда эти силы направлены:), и все).
любую силу можно разложить на сколько угодно других.
в данной задаче просят на радиальную и тангенциальную. вот это и надо сделать.

тем более, что никаких других данных не дано

если же надо разложить на 'двигающую' и 'вращающую', то все намного сложнее - надо учитывать и силу трения, и плечи, и, скорее всего, его массу.

Добавлено через 14 мин.

трения нет

тогда причем здесь:

Собственно изменение скоростей - линейной и угловой - под действием сил в течение промежутка времени dt происходит следующим образом:

Vx=Vx + dt * Fx / m

Vy=Vy + dt * Fy / m

W=W + dt * T / I

???

Вот собственно и вопрос - если на произвольную точку тела действует внешняя сила, как она отразится на линейной и угловой скоростях...

смотря какое тело, и где место соприкосновения.



Добавлено через 12 мин.

Тела - произвольные выпуклые многоугольники.

если правильно понимаю, тогда при ударе происходит "кантование" и силы приложены так:

, и нет никакого вращения, т.к. Тела - произвольные выпуклые многоугольники.

[Tony]

тогда причем здесь:
...
???

Ну вот взяли вы тело, и приложили к нему силу, чтобы оно с места сдвинулось... Что тут такого-то? Это симулятор ведь...

если правильно понимаю, тогда при ударе происходит "кантование" и силы приложены так:, и нет никакого вращения, т.к. Тела - произвольные выпуклые многоугольники.

При ударе тела обмениваются "импульсами" по нормали контакта... Этот метод придуман давно. Прикрепляю краткое описание.  GDC2006_Catto_Erin_PhysicsTutorial.ppt ( 582 килобайт ) Кол-во скачиваний: 5586

[sheka]

Ну вот взяли вы тело, и приложили к нему силу, чтобы оно с места сдвинулось... Что тут такого-то? Это симулятор ведь...

Это формулы с учетом силы трения. ускорение-то отрицательное! А для начальной скорости используются импульсы.

Прикрепляю краткое описание.

Да, спасибо, потом может как-то прочитаю, занятная методичка:).
С такой постановкой задачи тебе с головой хватит формулы m1v1=m2v2.

[Tony]

Это формулы с учетом силы трения. ускорение-то отрицательное! А для начальной скорости используются импульсы.

Не понял, при чем тут трение...

Да, спасибо, потом может как-то прочитаю, занятная методичка:).
С такой постановкой задачи тебе с головой хватит формулы m1v1=m2v2.

Боюсь, методичку вы даже не посмотрели . Я же написал "импульсы", а не _импульсы_. Как может закон сохранения импульсов учитывать "закручивание" тел? Тела - не какие-нибудь там шарики, а именно произвольные многоугольники... И в результате удара меняются как линейные, так и угловые скорости тел...

[Lapp]

я пишу программу - физический симулятор
...
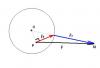
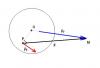
Если с линейной скоростью все понятно (если F=ma, то массы сократятся, а ускорение * время как раз и дает прирост скорости), то с угловой не очень...Получается, что T - это аналог F для вращательного движения, но получается, что T - скаляр, и как его назвать? Момент силы? Или нет?

Вот, теперь дело прояснилось)).
Цель вполне достойная, я поддерживаю и готов помочь, как с физикой так и с программированием.

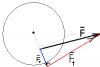
Да, называют его именно так: момент силы. В общем случае (в трехмерном пространстве) это есть вектор, но, как я понял, ты хочешь имплементить двумерный случай. А в двумерном случае могут осуществляться только два "типа" вращения: по часовой стрлке и против нее. То есть, если все же на секунду выскочить из двумерного пространства, это вращения вокруг оси, перпендикулярной нашему пространству (плоскости). И, соответственно, векторы угловой скорости, ускорения и моментов силы и импульса - все они направленны по одной оси, перпендикулярно этой плоскости. Таким образом, как угловая скорость, так и угловое ускорение, а с ними и момент силы - все они выражаются (каждое) только одним числом, которое является составляющей полного вектора каждой из них, взятой по оси, перпендикулярной плоскости (остальные две составляющих равны нулю). Это еще не дает права называть их скалярами - понятие скаляра несколько более сложно, нежели чем просто представление одним числом. Скорее тут справедливо сравнение со скоростью при рассмотрении движения по прямой (то есть одномерного движения). Там тоже скорость выражается одним числом, но ты же не станешь говорить, что в одномерном движении скорость есть скаляр - так? Если ты не знаком с вращательной механикой, советую тебе ее подучить - хотя, конечно, в двумерном случае можно обойтись этими обрывками - только не называй эти величины скалярами .

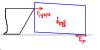
При рассмотрении взаимодействия тел к Закону сохранения имнульса (ЗСИ) тебе нужно добавить Закон сохранения момента импульса (ЗСМИ). Это совершенно незавмисимый закон в физике, то есть он не следует из ЗСИ, и тебе без него не обойтись. Если взаимодействие происходит мгновенно (назовем его соударением) и является упругим, то конечное состояние можно вывести без привлечения понятия силы, только на основе применения ЗСИ, ЗСМИ и ЗСЭ. Если же все же нужно рассматривать силы (взаимодействие растянуто во времени), то нужно рассматривать и их моменты относительно выбранной точки. Точка ЦМ во многих случаях удобна, но все же не обязательно использовать именно ее. Если честно, я прямо так с наскока не напишу сейчас все цепочки уравнений, которые тебе нужно запрограммировать, но в принципе это задача решаемая. Думаю, тебе нужно до конца разобраться с ними, прежде чем приступать к программированию. Пиши про свое продвижение и вопросы, я с удовольствием отвечу.
Успехов.

[Гость]

Думаю, тебе нужно до конца разобраться с ними, прежде чем приступать к программированию.

Если честно, сначала именно так и собирался сделать . Но потом обнаружил в сети "методичку" (сообщение №5), со всеми нужными формулами... Так что, собственно говоря, все это уже реализовано в виде программы (благо с программированием никаких проблем нет ) ...

Но теперь начинаю понимать, что цель была - не просто создание программы на основе готовых формул... Придется все-таки "учить матчасть". За объяснения насчет момента силы - спасибо.

Успехов.

Спасибо .