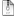Переборные Алгоритмы, Перебор Опции

[virt]

Существует особый класс задач ,в которых ответ может быть найден только полным перебором всех вариантов решения. Поэтому необходимо иметь некоторое представление о том как решаются подобные задачи.

1) задача о ферзях :
Условие :
на шахматной доске размера n*n расставить n ферзей так ,что-бы они не били друг друга.
Решение :
диагональ первого типа:
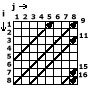
диагональ второго типа:

var
	{ признак занятости диагоналей первого типа }
	up: array[2 .. 16] of boolean;
	
	{ признак занятости диагоналей второго типа }
	down: array[-7 .. 7] of boolean;
	
	{ признак занятости вертикали }
	vert: array[1 .. 8]of boolean;
	
	{ номер вертикали, на которой стоит ферзь на каждой горизонтали }
	ihor: array[1 .. 8]of integer;
	n: integer;

{ проверка на допустимость хода в позицию (i,j) }
function d_hod(i, j: integer): boolean;
begin
	d_hod := vert[j] and up[i+j] and down[i-j];
end;

procedure hod(i, j: integer); { сделать ход }
begin
	ihor[i] := j;
	vert[j] := false;
	up[i+j] := false;
	down[i-j] := false;
end;

procedure o_hod(i, j: integer); { отменить ход }
begin
	vert[j] := true;
	up[i+j] := true;
	down[i-j] := true;
end;

Нахождение одного варианта расстановки :

procedure find_one(i: integer; var q: boolean);
var j: integer;
begin
	j:=0;
	repeat
		inc(j);
		q:=false;
		if d_hod(i, j) then begin
			hod(i,j);
			if i < n then begin
				find_one(i+1,q);
				if not q then o_hod(i,j);
			end
			else q:=true;
		end;
	until q or (j=n);
end;

Нахождение всех решений :

procedure print;
var i: integer;
begin
	write('  ',s,'   ');for i:=1 to n do write(ihor[i],' ');
	writeln;
end;

procedure find_all(i: integer);
var j: integer;
begin
	if i<=n then begin
		for j:=1 to n do
			if d_hod(i,j) then begin
				hod(i,j);
				find_all(i+1);
				o_hod(i,j);
			end;
	end
	else begin
		inc(s);
		print;
	end;
end;

2) задача о шахматном коне :
Условие :
Найти количество всех вариантов обхода шахматной доски конем.
Решение :

program kon_in_nm_matr_full_variants;
const
	_maxnm=8;
	dx: array[1 .. 8] of integer = (-2,-1,1,2,2,1,-1,-2);
	dy: array[1 .. 8] of integer = (1,2,2,1,-1,-2,-2,-1);
var
	a: array[-1 .. _maxnm+2, -1 .. _maxnm+2] of integer;
	n, m, i, j: integer;
	t: longint;

procedure solve(x, y, l: integer);
var k, i, j: integer;
begin
	a[x, y] := l;
	if l = n*m then inc(t)
	else
		for k:=1 to 8 do begin
			i:=x+dx[k];j:=y+dy[k];
			if a[i,j] = 0 then solve(i, j, l+1);
		end;
	a[x,y] := 0;
end;

begin
	readln(n, m);
	for i:=-1 to n+2 do a[i,-1]:=-1;
	for i:=-1 to n+2 do a[i,0]:=-1;
	for i:=-1 to n+2 do a[i,m+1]:=-1;
	for i:=-1 to n+2 do a[i,m+2]:=-1;
	for j:=1 to m do a[-1,j]:=-1;
	for j:=1 to m do a[0,j]:=-1;
	for j:=1 to m do a[n+1,j]:=-1;
	for j:=1 to m do a[n+2,j]:=-1;
	for i:=1 to n do
		for j:=1 to m do a[i,j]:=0;

	t := 0;
	for i:=1 to n do
		for j:=1 to m do begin
			solve(i,j,1);
		end;
	writeln('   ', t);
end.

Условие :
Найти один вариант обхода методом Варнсдорфа.
Суть метода : при обходе коня следует ставить на поле ,из которого он может сделать минимальное количество перемещений на еще не занятые поля.
Решение :

program kon_in_nm_matr_one_variant;
const
	_maxnm=8;
	dx: array[1 .. 8] of integer = (-2,-1,1,2,2,1,-1,-2);
	dy: array[1 .. 8] of integer = (1,2,2,1,-1,-2,-2,-1);
var
	a: array[-1 .. _maxnm+2, -1 .. _maxnm+2] of integer;
	n, m, i, j: integer;

procedure solve(x, y, l: integer);
var
	w: array[1 .. 8] of integer;
	xn, yn, i, j, m1: integer;
begin
	a[x,y] := l;
	if l=n*m then begin
		writeln;
		for i:=1 to n do begin
			for j:=1 to m do write(a[i,j],'   ');
			writeln;
		end;
		halt;
	end
	else begin
		for i:=1 to 8 do begin
			w[i]:=0;
			xn:=x+dx[i];
			yn:=y+dy[i];
			if a[xn,yn]=0 then begin
				for j:=1 to 8 do
					if a[xn+dx[j],yn+dy[j]]=0 then inc(w[i]);
			end
			else w[i]:=-1;
		end;
		i:=1;
		while i<=8 do begin
			m1:=1;
			for j:=2 to 8 do
				if w[j]<w[m1] then m1:=j;
			if (w[m1]>=0) and (w[m1]<maxint) then
				solve(x+dx[m1],y+dy[m1],l+1);
			w[m1]:=maxint;
			inc(i);
		end;
	end;
	a[x,y]:=0;
end;

begin
	readln(n,m);
	for i:=-1 to n+2 do a[i,-1]:=-1;
	for i:=-1 to n+2 do a[i,0]:=-1;
	for i:=-1 to n+2 do a[i,m+1]:=-1;
	for i:=-1 to n+2 do a[i,m+2]:=-1;
	for j:=1 to m do a[-1,j]:=-1;
	for j:=1 to m do a[0,j]:=-1;
	for j:=1 to m do a[n+1,j]:=-1;
	for j:=1 to m do a[n+2,j]:=-1;
	for i:=1 to n do
		for j:=1 to m do a[i,j]:=0;
	for i:=1 to n do
		for j:=1 to m do begin
			solve(i,j,1);
		end;
end.

3)задача о лабиринте :
Условие :
Дано клеточное поле, некоторые клетки заняты препятствиями. Найти количество путей от начальной точки до конечной.
Решение :

program labirint_way;
const
	_maxn=30;
	dx: array[1 .. 4] of integer = (1,0,-1,0);
	dy: array[1 .. 4] of integer = (0,1,0,-1);
var
	a: array[0 .. _maxn+1, 0 .. _maxn+1] of integer;
	xn, yn, xk, yk: integer;
	i, j, n: integer;
	t: longint;

procedure solve(x, y, k: integer);
var i: integer;
begin
	a[x,y]:=k;
	if (x=xk) and (y=yk) then inc(t)
	else
		for i:=1 to 4 do
			if a[x+dx[i],y+dy[i]]=0 then solve(x+dx[i],y+dy[i],k+1);
	a[x,y]:=0;
end;

begin
	{ Подправлена инициализация матрицы... }
	for i := 0 to _maxn+1 do
		for j := 0 to _maxn+1 do a[i, j] := 1;
	read(n);
	for i:=1 to n do
		for j:=1 to n do read(a[i,j]);
	readln(xn,yn,xk,yk);
	t:=0;
	solve(xn,yn,1);
	writeln(t);
end.

4)задача о парламенте :
Условие :
На некотором демократическом острове каждый из жителей организовал партию которую и возглавил. В каждой партии кроме президента оказался еще как минимум один член. Составить самый малочисленный парламент, в котором будут представлены члены всех партий.
Решение :

const maxn = 150;
type
	zint=0 .. maxn+1;
	zset = set of 0 .. maxn;
	person=record
		man: zint;
		num_part: zint;
		part: zset;
	end;

var
	a: array[zint] of person;
	n, mn, min, i: zint;
	rwork, rbest: zset;

{ ... }
procedure include(k: zint);
begin
	rwork:=rwork+[a[k].man];
	inc(mn);
end;

procedure exclude(k: zint);
begin
	rwork:=rwork-[a[k].man];
	dec(mn);
end;

procedure solve(k: zint; res, rt: zset);
var i: zint;
begin
	if rt=[] then begin
		if mn<min then begin
			min:=mn;
			rbest:=rwork;
		end;
	end
	else begin
		i:=k;
		while i<=n do begin
			include(i);
			solve(i+1,res+a[i].part,rt-a[i].part);
			exclude(i);
			inc(i);
		end;
	end;
end;

begin
	init;
	solve(1, [], [1..n]);
	for i:=1 to n do
		if i in rbest then write(i,' ');
end.

5)задача о рюкзаке :
Условие :
Дано - максимальный вес рюкзака. Дано n предметов имеющих свой вес и стоимость. Определить максимальную стоимость груза, вес которого не превышает максимального веса рюкзака.
Решение :

program rukzak_perebor;
const maxn = 20;
var
	n, w: integer;
	weight, price: array[1 .. maxn] of integer;
	best, now: array[1 .. maxn] of integer;
	maxprice: longint;

procedure init;
var i: integer;
begin
	read(n);
	read(w);
	for i:=1 to n do read(weight[i]);
	for i:=1 to n do read(price[i]);
end;

procedure rec(k, w: integer; st: longint);
var i: integer;
begin
	if (k>n) and (st>maxprice) then begin
		best:=now;
		maxprice:=st;
	end
	else
		if k<=n then
			for i:=0 to w div weight[k] do begin
				now[k]:=i;
				rec(k+1,w-i*weight[k],st+i*price[k]);
			end;
end;

begin
	init;
	rec(1, w, 0);
	writeln('   ',maxprice);
end.

Сообщение отредактировано: volvo - 27.01.2009 2:19

[virt]

6) задача о коммивояжёре :
Условие :
Имеется n городов, расстояния между которыми заданы. Коммивояжеру необходимо выйти из какого-то города, побывать во всех остальных n-1 городах точно по одному разу, и вернуться в исходный город. Маршрут должен быть минимальным по длине.
Решение :

const maxv = 100;
var
	{ матрица расстояний между городами }
	a: array[1 .. maxv, 1 .. maxv] of integer;
	b: array[1 .. maxv, 1 .. maxv] of byte;
	way, best: array[1 .. maxv] of byte;
	
	{ был ли коммивояжер в данном городе }
	nnew: array[1 .. maxv] of boolean;
	bestcost: integer;
	n, i: integer;

{ ... }

{
	сортируем каждую строку матрицы А по возрастанию
	расстояний. Однако сами элементы матрицы А не
	переставляем ,а изменяем в матрице B номера столбцов
	матрицы А.
}
procedure sortlines;	
var
	k, i, j: integer;
	w: integer;
begin
	for i:=1 to n do
		for j:=1 to n do b[i,j]:=j;
	for k:=1 to n do
		for i:=1 to n-1 do
			for j:=i+1 to n do
				if a[k,b[k,i]]>a[k,b[k,j]] then begin
					w:=b[k,i]; b[k,i]:=b[k,j]; b[k,j]:=w;
				end;
end;

procedure solve(v, count: byte; cost: integer); { основная процедура }
var i: integer;
begin
	if cost > bestcost then exit;
	if count=n then begin
		cost:=cost+a[v,1];
		way[n]:=v;
		if cost<bestcost then begin
			bestcost:=cost;
			best:=way;
		end;
		exit;
	end;
	nnew[v]:=false;
	way[count]:=v;
	for i:=1 to n do
		if nnew[b[v,i]] then solve(b[v,i],count+1,cost+a[v,b[v,i]]);
	nnew[v]:=true;
end;

begin
	init;
	sortlines;
	solve(1,1,0);
	writeln(bestcost:4); { вывод результата }
	for i:=1 to n do write(best[i],' '); writeln;
end.