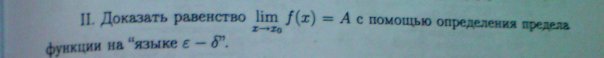|
Хорошо, давай сначала .
Делаем замену y=-3+x (тогда x-x0 = x-3 = y).
Преобразуем разность функций:
ctg(2(-3+y)+9) - ctg(3) =
ctg(3+2y) - ctg(3) =
cos(3+2y) / sin(3+2y) - cos(3) / sin(3) =
(cos(3+2y)*sin(3) - cos(3)*sin(3+2y)) / sin(3+2y) / sin(3) =
sin(2y) / (sin(3)*cos(2y)+cos(3)*sin(2y)) / sin(3)
Теперь выберем произвольное e (эпсилон). Наша задача: найти такое d (дельта), чтобы при любом y, удовлетворяющем условию 0<y<d выполнялось и
|sin(2y) / (sin(3)*cos(2y)+cos(3)*sin(2y))| / |sin(3)| < e .
С учетом, что sin(3)>0 :
|sin(2y) / (sin(3)*cos(2y)+cos(3)*sin(2y))| < e*sin(3) .
Поскольку обе стороны неравенства больше нуля, переворачиваем его (единицу делим на стороны со сменой знака неравенства) :
|sin(3)*cos(2y)/sin(2y) + cos(3)| > 1 / (e*sin(3)) .
Используем свойство модуля |a-b| => |a| - |b| , завышаем требования:
|sin(3)*cos(2y)/sin(2y)| - |cos(3)| > 1 / (e*sin(3))
- если выполнено это, то выполнено и то.
Так как cos(3)~-0.99<0, то |cos(3)|=-cos(3). Переносим его вправо:
|sin(3)*cos(2y)/sin(2y)| > 1/e/sin(3) - cos(3)
Так как sin(3)~0.14>0 , то:
|cos(2y)/sin(2y)| > (1/e/sin(3) - cos(3)) / sin(3) = M
- обозначим M для простоты.
Еше раз переворачиваем:
|sin(2y)/cos(2y)| < 1/M .
Выберем d<Pi/6 , тогда cos(2y)>1/2>0
Получаем:
|sin(2y)| < cos(2y)/M .
Снова загрубляем, заменяя косинус на 1/2:
|sin(2y)| < 1/2/M.
Используя |sin(x)|<=|x| , снова загрубляем неравенство:
|2y| < 1/2/M ,
или:
|y| < 1/4/M
- снова, если выолнено это, то выполнено и то.
Это значит, что можно взять d=1/4/M , то есть:
d = sin(3) / (1/e/sin(3) - cos(3)) / 4 .
Осталось пересечь с наложенным ранее условием d<Pi/6, и это и есть искомая дельта.
Надеюсь, не ошибся в арифметике . Отвык я от нее..
Добавлено через 10 мин.
Стремление синуса к нулю эквивалентно в определенном смысле неравенству |sin(x)|<|x|, которое использовано в методичке. Так что я свел к нему.
--------------------
я - ветер, я северный холодный ветер
я час расставанья, я год возвращенья домой
|