Помогите написась програму Квадрат, Нужна очень срочно Опции

[Yara]

Треугольник задан кординатами вершын (x1,y1),(x2,y2),(x3,y3). Найти л длину стороны квадрата, в какой вписан треугольник, так чтобы все вершыни треугольника лежали в средини или на сторонах квадрата.
буду рав если подскажете математическое решение!!!

помогите пожалуста. если можна поскорее!!!!

М

Раз математическое - то тебе пока сюда... Разбирайся с алгоритмом. Потом будешь реализовывать... volvo

[klem4]

чтобы все вершыни треугольника лежали в средини или на сторонах квадрата.

В середине для треуголника вписанного в квадрат - понятие растяжимое, имхо), если сказанное тобой или - не исключающее, хотя задание если честно вообще мутновато звучит, то имхо сторона квадрата = ниабольшей по длине cтороне тругольника, он (треуголник) тогда в такой квадрат полюбому войдет.

Добавлено через 16 мин.
Точнее даже наверное так: Наиболшая сторона треуголника == диагонали квадрата ... Сторону теперь получить не сложно ;)

[TarasBer]

Наибольшая сторона = диагональ квадрата? Треугольник не факт тупоугольный.

[klem4]

Да, если взять скажем равносторонний, то он не впишется ...

Значит пока как вариант, сторона квадрата = наибольшей стороне треуголника, хотя можно смотреть какой вид треуголника из из этого уже исходить.

Надо думать, но пажалуй завтра.

[мисс_граффити]

извращенкой не называйте...
думаю, алгоритм далек от идеала, но....
1. ищем радиус описанной окружности
2. сторона квадрата - диаметр.

радиус описанной можно искать через площадь: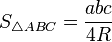

с другой стороны - формула Герона или вот такая формула:

осталось выразить, но это легкая задача.

правда, возможны случаи, когда этот квадрат не будет наименьшим возможным

Сообщение отредактировано: мисс_граффити - 27.02.2007 5:38

[Lapp]

Во-первых, я все же сформулирую условие почетче - так, как я его понял. Если автор темы обнаружит неточности или ошибки - пусть поправит.

Найти наименьший квадрат, содержащий заданный треугольник.

Если понимать задачу именно так, то, имхо, решить ее непросто.. Аналитического решения я не вижу. С алгоритмическим тоже непросто, мне кажется. После некоторых раздумий, я решил, что можно опираться на одно утверждение (лемму ), а именно (я разбио его на две части) :

1. Если искомый квадрат найден, то одна из его вершин совпадает с вершиной треугольника (или они могут быть совмещены с выполнением условий).
2. Упомянутая вершина треугольника - та, в которой встречаются две наиболее длинные стороны его.

Алгоритм напрашивается следующий:
Берем вершину тр-ка, в которой встречаются две длинные стороны, и рисуем из нее два луча под прямым углом друг к другу. Затем проводим две прямые, параллельные им, через точки, принадлежащие треугольнику, наиболее удаленные от начальных лучей (соответственно от первого и второго). Проверяем полученный прямоугольник на равенство сторон.

Громоздко, однако.. Надо еще подумать.

[T i m e]

чтобы все вершыни треугольника лежали в средини или на сторонах квадрата

Я так понял, что каждая из трёх вершин может лежать или в любом месте на стороне квадрата, либо на серединном перпендикуляре к стороне квадрата... А то если у нас только первое условие дано, то действительно для равностороннего треугольника квадрат никак не получится. Хороше бы конечно, чтобы Yara сам пояснил чё к чему, а то я смотрю тут все теряются в догадках...